Magnetic fields are generated by moving charges or magnetic materials. Magnetic fields act on moving charges and currents. A Tesla (T) which is equivalent to 
is the unit of a magnetic field strength. Magnetic fields can be added in superposition because they are vector fields.
The Lorentz force on the charged particle in the electromagnetic field is
|
(I.1) |
The magnetic force on the piece of the current 
is
|
(I.2) |
(here 
gives both the magnitude and direction of the small piece of the current-carrying wire).
Ampere’s law in integral and differential form is
|
(I.3) |
where 
, 
is the current encircled by the contour, and 
is the current density. The magnetic field also satisfies
|
(I.4) |
This is a statement that there are no magnetic monopoles, or, equivalently, that magnetic field lines have no endings – i.e. closed lines (compare with electric field lines).
The magnetic field at distance 
from a current 
in a long straight wire points in the tangential direction and has magnitude
 |
(I.5) |
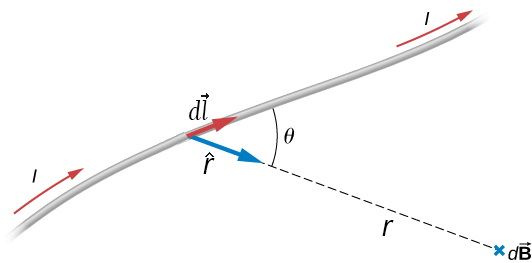
The contribution to the magnetic field from a piece of a wire 
carrying current I is given by the Biot-Sarart law (Figure I.1):
|
(I.6) |
The Biot-Sarart law is valid for steady currents and can be used to calculate magnetic fields due to current-carrying wires of various shapes. For example, the magnetic field due to wire in the shape of a ring of radius b at distance z from the center of the ring along the ring’s axis of symmetry is directed along the symmetry axis and has the magnitude
|
(I.7) |
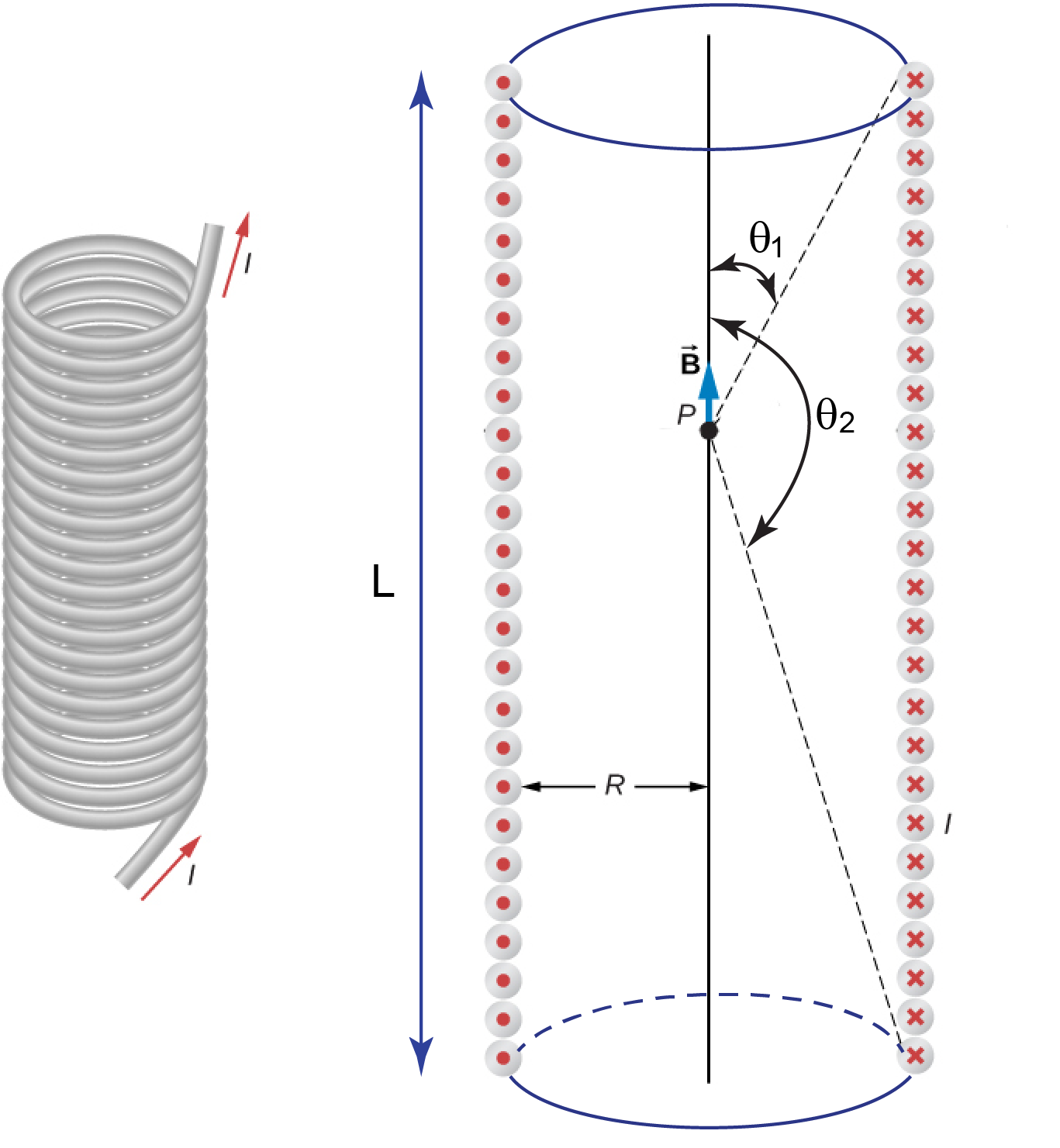
The Biot-Sarart law may also be used to calculate the magnetic field of the cylindrical coil of wire – solenoid. For the solenoid with number of turns in the winding, per unit length 
, current 
, the magnetic field at point 
(see Figure I.2) is
|
(I.8) |
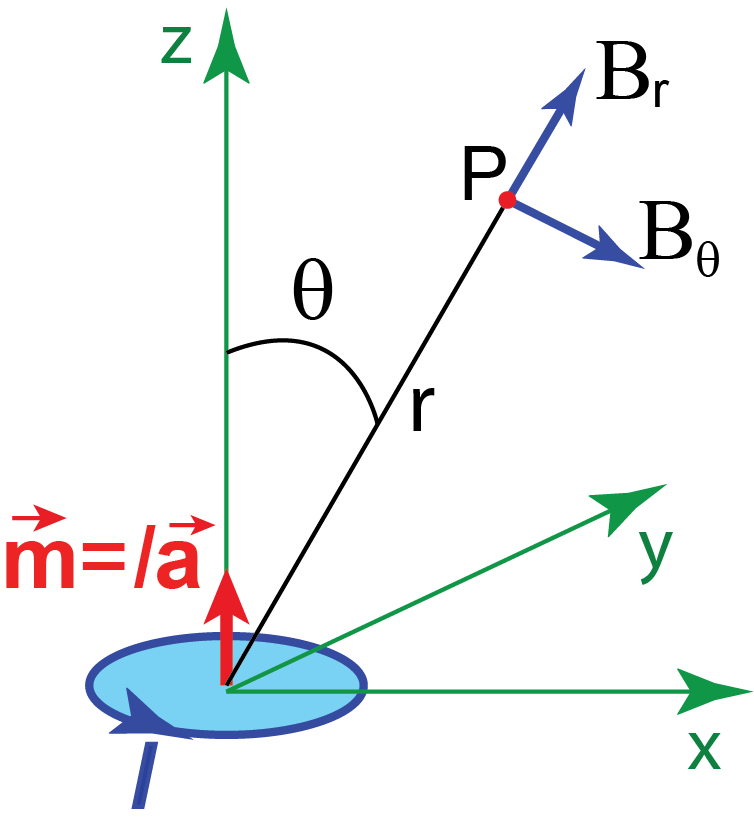
All loops (not necessarily circular) with the same 
product produce the same magnetic field very far from the loop (far field). The product 
is called the magnetic dipole moment of the current loop: 
. The direction of 
is normal to the loop and is related to the direction of the current in the loop by a right-hand-screw rule (see Figure I.3).
Far field of the magnetic dipole 
in polar coordinates is
|
(I.9) |
, 
, 
In Cartesian coordinate this magnetic field is
|
(I.10) |
, 
, 
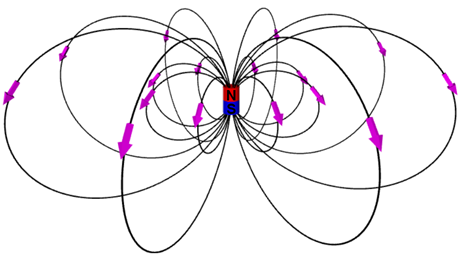
The example of the magnetic field lines of a magnetic dipole (i.e. a small magnet, or a small loop of current) is shown in Figure I.4. The far field expressions (I.9) and (I.10) for the magnetic dipole are applicable not only for the current loops but also for permanent magnets. Magnetic field lines of permanent magnet are directed from the North pole to the South pole of the magnet (see Figures I.4 and I.5). The magnetic dipole moment always points from the South to the North pole.
The energy of a magnetic dipole in the magnetic field is
|
(I.11) |
The force on a magnetic dipole in the magnetic field is
 |
(I.12) |
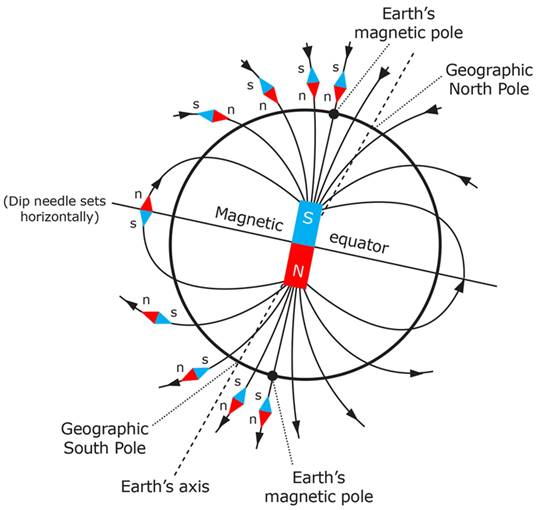
Earth's magnetic field (see Figure I.6) is generated by electric currents due to the motion of convection currents of molten iron in the Earth's outer core. The magnitude of the Earth's magnetic field at its surface ranges from 25 to 65 
. As an approximation, it is represented by a field of a magnetic dipole currently tilted at an angle of about 11 degrees with respect to Earth's rotational axis, as if there were a bar magnet placed at that angle at the center of the Earth.
The North geomagnetic pole, currently located near Greenland in the northern hemisphere, is actually the south pole of the Earth's magnetic field, and conversely.
In this lab we will determine latitude of our location using the Earth’s magnetic field. In geography, latitude (see Figure I.7) 