Lab 7.
Electromagnetic Induction: Magnet falls inside a conducting tube.
Introduction.

Faraday discovered that a wire with a changing current can induce a current in a nearby wire. He determined that any change in magnetic flux through the loop induces emf in it:

(I.1)

The emf and associated current is generated through an electric field inside the wire that is described by the last equality in the equation above, where C is the curve that bounds the surface S. The differential form of Faraday's Law is given by

(I.2)

 

Faraday's Law gives the amplitude of the emf, but Lenz's Law gives the direction of the induced current. It states that the induced current creates an induced magnetic field that opposes the change in magnetic flux.

If we have two circuits C₁ and C₂, a current  in circuit C₁ will produce a flux  through the other circuit. The mutual inductance  is defined by

(I.3)

It then follows that changing  produces an emf in C₂ equal to

(I.4)

Similarly, a current  in circuit C₂ will produce a flux  through the circuit C₁. The mutual inductance  is defined by

(I.5)

The two coefficients of mutual inductance are symmetric:

(I.6)

A current I in a circuit will produce a flux  through the circuit. The self-inductance of this circuit is defined by . The emf induced in this circuit is then

(I.7)

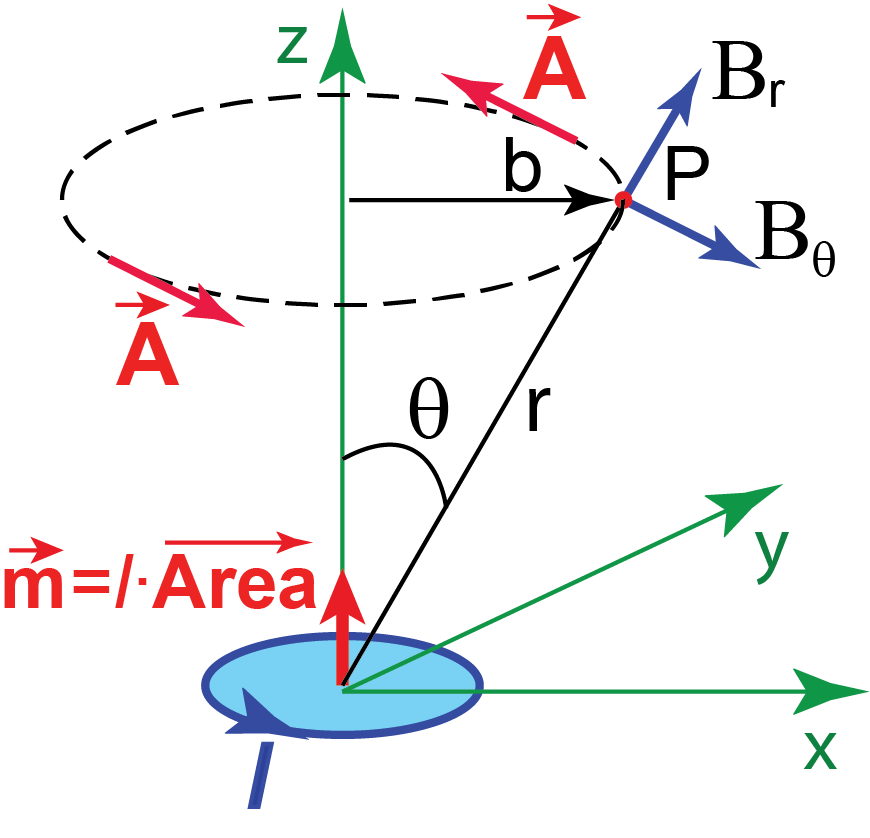
Magnetic dipole moment  of the current loop is a vector, its direction is that of the directed area of the region surrounded by the loop:

Far field of the magnetic dipole  in polar coordinates is (see Figure I.1):

,      ,            (I.8)

In Cartesian coordinates (assuming setup in Figure I.1) this magnetic field is:

,   ,    (I.9)

Vector potential of the magnetic dipole   located on the z axis is tangent to the horizontal circle with the center on z axis. Its magnitude is:

(I.10)

Since  using Stokes’ theorem we obtain the flux of the magnetic field of the magnetic dipole through the circle of radius b with the center on z axis (see Figure I.1):

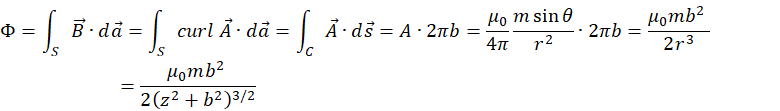(I.11)